
Class 12 Maths Additional Practice Questions Paper 2023-24: The Central Board of Secondary Education (CBSE) has issued the Class 12 Maths Additional Practice Questions Paper 2023-24 for students in Class 12 who have selected PCM as their main subject. To access the CBSE Class 12 Maths Additional Practice Questions Paper 2023-24 (CBSE), students can visit the official CBSE website @cbseacademic.nic.in.
It is essential for students preparing for the CBSE Class 12 exam to download and go through the CBSE Class 12 Maths Additional Practice Paper 2023-24 PDF before taking the actual board exam. These practice papers will aid students in comprehending and getting accustomed to the recently updated format of the Class 12 board exams. The CBSE Class 12 Maths Additional Practice Question Paper 2023-24 is provided in the article below.
Q 1. For any 2 × 2 matrix P, which of the following matrices can be Q such that PQ = QP?
 Ans:
(b)
Ans:
(b)
Q 2. V is a matrix of order 3 such that |adj V| = 7. Which of these could be |V|?
(a)- 7² (b)- 7 (c)- √7 (d)- ³√7 Ans: (c) √7Q 3: The points D, E, and F are the mid-points of AB, BC, and CA respectively.
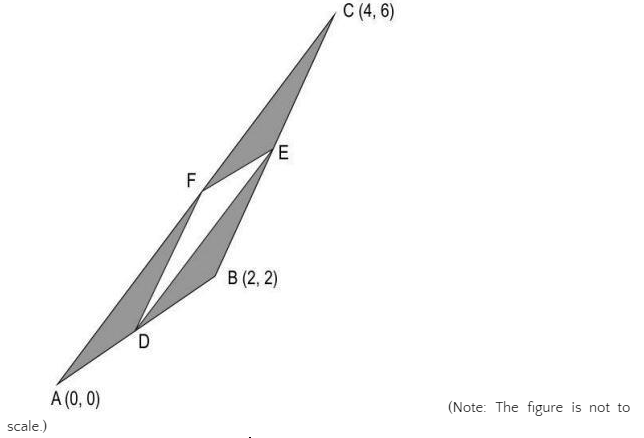
(Note: The figure is not to scale.)
What is the area of the shaded region? (a) 2 sq units
(b) 3/2 sq units (c) 1/2 sq units (d) (2√26 – 1) sq units Ans: (b) 3/2 sq unitsQ 4: If f(x) = cos-1√x, 0 < x < 1, which of the following is equal to F (x)?
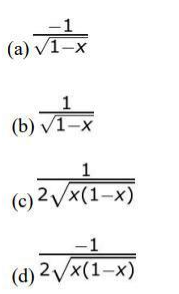 Ans:
(d)
Ans:
(d)
Q 5: A function f: R -> R is defined by:
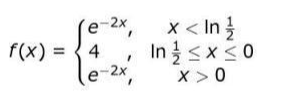
Which of the following statements is true about the function at the point x = ln 1/2? (a) f(x) is not continuous but differentiable.
(b) f(x) is continuous but not differentiable. (c) f(x) is neither continuous nor differentiable. (d) f(x) is both continuous as well as differentiable. Ans: (b) f(x) is continuous but not differentiable.Q 6. In which of these intervals is the function f(x) = 3x² – 4x strictly decreasing? (a) (-∞, 0)
(b) (0, 2) (c) (2/3, ∞) (d) (-∞, ∞) Ans: (a) (-∞, 0)Q 7. Which of these is equal to ∫ 𝑒(𝑥log 5) 𝑒𝑥𝑑𝑥, where C is the constant of integration?
(a) (5e) 𝑥 /log 5e + C (b) log 5 𝑥 + x + C (c) 5 𝑥 e 𝑥 + C (d) (5e) 𝑥 log x + C Ans: (5e) 𝑥 /log 5e + CQ 8. Shown below is the curve defined by the equation y = log (x + 1) for x ≥ 0.
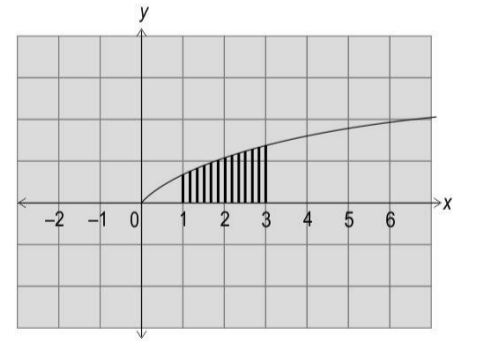
Which of these is the area of the shaded region? (a) 6log(2) – 2
(b) 6log(2) – 6 (c) 6log(2) (d) 5log(2) Ans: (a) 6log(2) – 2Q 9. In which of the following differential equations is the degree equal to its order?
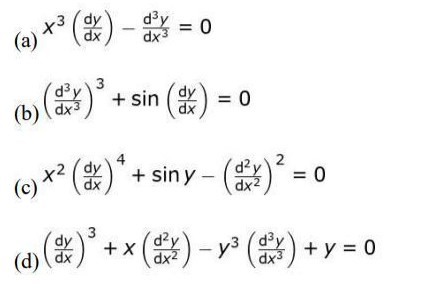 Ans:
(c)
Ans:
(c)
Q 10. Kapila is trying to find the general solution of the following differential equations.
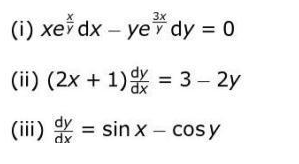
Which of the above becomes variably separable by substituting y = b.x, where b is a variable? (a) only (i)
(b) only (i) and (ii) (c) all – (i), (ii) and (iii) (d) None of the above. Ans: (a) only (i).Q 11. Find the domain of the function y = cos–¹(|x – 1|). Show your steps.
Solution: Since the domain of the inverse of the cosine function is [-1, 1], find the domain of the given function as follows: -1 ≤ x – 1 ≤ 1 So, 0 ≤ x ≤ 2 And, -1 ≤ 1 – x ≤ 1 => 1 ≥ x – 1 ≥ -1 So, 2 ≥ x ≥ 0 Concludes the domain of cos–¹(|x – 1|) as [0, 2].OR
Q 11. Draw the graph of the following function: y = 2sin–¹(x), -π ≤ y ≤ π
Solution: Draw the graphs of y = 2sin–¹(x) as shown below.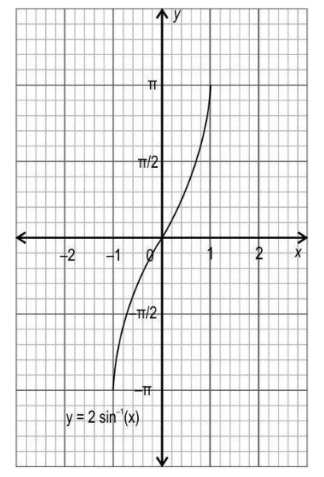
Q 12.

Solution:
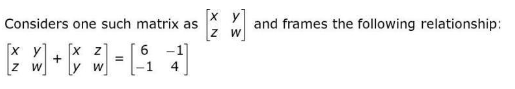 Obtains x = 3 and w = 2 using the relationship obtained in the previous step as
follows:
2x = 6 => x = 3
2w = 4 => w = 2
Writes any value of y and z that satisfies the third relationship obtained in the first
step. For example, y = 0 and z = -1.
Obtains x = 3 and w = 2 using the relationship obtained in the previous step as
follows:
2x = 6 => x = 3
2w = 4 => w = 2
Writes any value of y and z that satisfies the third relationship obtained in the first
step. For example, y = 0 and z = -1.

(Award full marks for any other matrix that satisfies the relationship.)
Q 13. If x = cot t and y = cosec²t, find:
(i) dy/dx (ii) d²y/dx²Show your steps.
Solution:

(Award full marks if any alternate method is used.)
Q 14. Solve the integral:
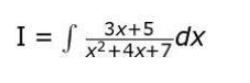
Show your work.
Solution: Rewrites the numerator of the given integral as: 3x + 5 = A 𝑑 / 𝑑𝑥 (x² + 4x + 7) + B => 3x + 5 = A(2x + 4) + B Finds the values of A and B by comparing the coefficients of like terms as: 2A = 3 => A = 3/2 4A + B = 5 => B = -1 Substitutes the values of A and B in the given integral and integrates the same as: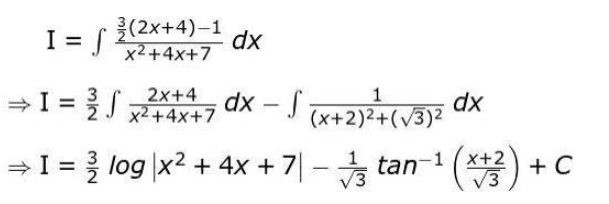 where C is the constant of integration.
where C is the constant of integration.
Q 15. Evaluate the integral:
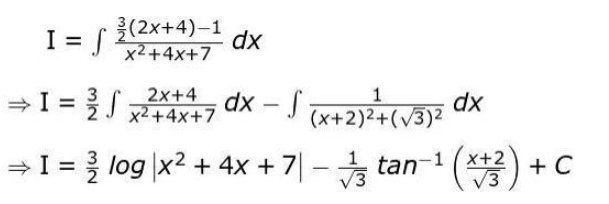
Show your steps.
Solution: Takes u = (25 + cos θ). Finds du as: du = -sin θ dθ Finds the change in limit when θ = 0 and θ = 𝜋 /2 to u = 26 and u = 25 respectively Rewrites the given integral using the above substitution and integrates the same as: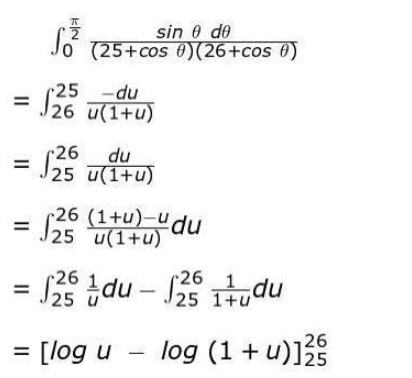 Applies the limit to find the value of the given definite integral as log 26 ×26/25 ×27
(Award full marks if the problem is solved correctly by taking u = 26 + cos θ.)
Applies the limit to find the value of the given definite integral as log 26 ×26/25 ×27
(Award full marks if the problem is solved correctly by taking u = 26 + cos θ.)
OR
Q 15. Using the properties of definite integrals, prove the following:
State the property used.
Solution: States the property that is going to be used as: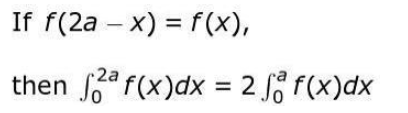 Takes 2a = π and f(x) = h(sin x).
Finds f(2a – x) as:
f(2a – x) = f(π – x) = h(sin(π – x)) = h(sin x) = f(x)
Thus confirms that the property listed in the above step can be applied to the given integral.
Hence concludes that:
Takes 2a = π and f(x) = h(sin x).
Finds f(2a – x) as:
f(2a – x) = f(π – x) = h(sin(π – x)) = h(sin x) = f(x)
Thus confirms that the property listed in the above step can be applied to the given integral.
Hence concludes that:
Q 16. When an object is thrown vertically upward, it is under the effect of gravity and air resistance. For small objects, the force due to air resistance is numerically equal to some constant k times v, where v is the velocity of the object (in m/s) at time t (s).
This situation can be modelled as the differential equation shown below.

A tennis ball of mass 0.050 kg is hit upwards with a velocity of 10 m/s. An air resistance numerically equal to 0.4v acts on the ball.
(i) Model the above situation using a differential equation. (ii) Write an expression for the velocity of the ball in terms of time.Show your work.
Solution: (i) Models the situation and rearranges terms to form a linear differential equation as follows: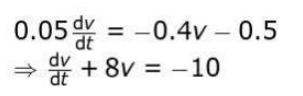 (ii)
Considering the obtained equation as linear of the form
𝑑𝑦
/
𝑑𝑥
+ Py = Q with P = 8 and hence takes the integrating factor as:
(ii)
Considering the obtained equation as linear of the form
𝑑𝑦
/
𝑑𝑥
+ Py = Q with P = 8 and hence takes the integrating factor as:
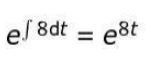 Multiplies the differential equation by the integrating factor as follows:
Multiplies the differential equation by the integrating factor as follows:
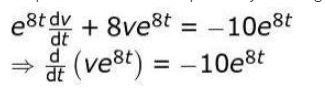 Integrates both sides to obtain the general solution of the differential equation as follows:
Integrates both sides to obtain the general solution of the differential equation as follows:
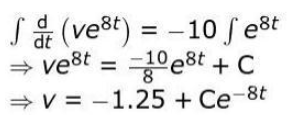 Where C is the constant of integration.
Uses the initial condition v(0) = 10 m/s to find the value of C as follows:
10 = -1.25 + C
⇒
C = 11.25
Hence, write the expression for the velocity of the ball as a function of time as follows:
v = -1.25 + 11.25e-8t
Where C is the constant of integration.
Uses the initial condition v(0) = 10 m/s to find the value of C as follows:
10 = -1.25 + C
⇒
C = 11.25
Hence, write the expression for the velocity of the ball as a function of time as follows:
v = -1.25 + 11.25e-8t
Q 17. The Earth has 24 time zones, defined by dividing the Earth into 24 equal longitudinal segments. These are the regions on Earth that have the same standard time. For example, the USA and India fall in different time zones, but Sri Lanka and India are in the same time zone.
A relation R is defined on the set U = {All people on the Earth} such that R = {(x, y)| The time difference between the time zones x and y resides in 6 hours}.
Show your work.
Solution: i) Writes that for no x ∈ U, (x, x) ∈ R as the difference in time between x & x is 0 hours. Concludes that R is not reflexive. Write that, whenever the difference in time between x and y is 6 hours, the difference in time between y and x is also 6 hours. That is, (x, y) ∈ R => (y, x) ∈ R. Concludes that R is symmetric. Write that, if the difference in time between x and y is 6 hours, and the difference in time between y and z is also 6 hours, then the difference in time between x and z could be either 0 hours or 12 hours. That is, (x, y) ∈ R & (y, z) ∈ R but (x, z) ∉ R. Concludes that R is not transitive. ii) From the above steps, concludes that R is not an equivalence relation.OR
Q 17. A function f : R – {-1, 1} -> R is defined by:
f (x) = x / x² – 1
Show your work.
Solution: i) Assumes f(x) = f(y) and evaluates the same as: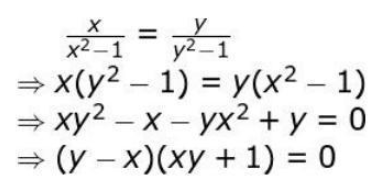 Uses the above step to conclude that x = y or xy = -1.
Take a pair of numbers x and y such that xy = -1 to show that f is not one-one.
For example,
for x = 1/2 and y = -2, f(x) = − 2/3 and f(y) = − 2/3.
ii)
Equates f(x) to y and solves the same to express x in terms of y as:
Uses the above step to conclude that x = y or xy = -1.
Take a pair of numbers x and y such that xy = -1 to show that f is not one-one.
For example,
for x = 1/2 and y = -2, f(x) = − 2/3 and f(y) = − 2/3.
ii)
Equates f(x) to y and solves the same to express x in terms of y as:
 Write that for any y
∈
R (codomain), there exists x
∈
R – {-1, 1} (domain) such that f(x) = y. Hence concludes that f is onto.
Write that for any y
∈
R (codomain), there exists x
∈
R – {-1, 1} (domain) such that f(x) = y. Hence concludes that f is onto.
Q 18. Abdul threw a basketball in the direction of the basketball hoop which traversed a parabolic path in a vertical plane as shown below.
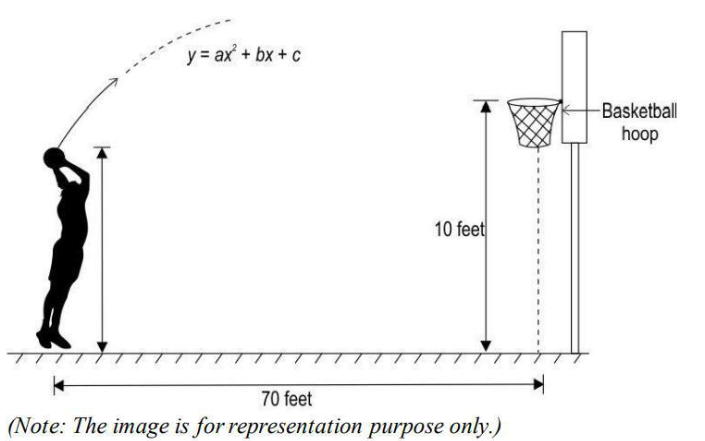
The equation of the path traversed by the ball is y = ax2 + bx + c with respect to a xy-coordinate system in the vertical plane. The ball traversed through the points (10, 16), (20, 22) and (30, 25). The basketball hoop is at a horizontal distance of 70 feet from Abdul. The height of the basketball hoop is 10 feet from the floor to the top edge of the rim.
Did the ball successfully go through the hoop? Justify your answer.
(Hint: Consider the point where Abdul is standing as the origin of the xy-coordinate system.)
Solution: Writes the system of equations as: 100a + 10b + c = 16 400a + 20b + c = 22 900a + 30b + c = 25 Write the above system of equations in the form AX = B as:
(Award 1 mark if only all the cofactors are found correctly.)
Finds the values of a, b and c as − 3/200, 21/20and 7 respectively by solving X = A-1B as: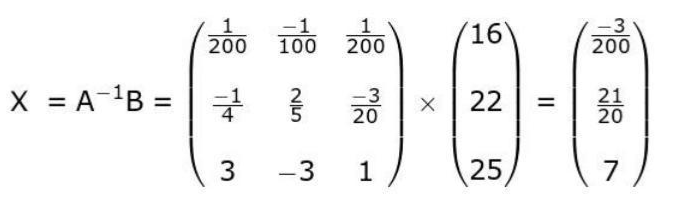 Finds the equation of the path traversed by the ball as:
y = − 3/200 x² + 21/20 x + 7.
Write that when x = 70 feet, y = 7 feet. So, the ball went by 7 feet above the floor which means 3 feet below the basketball hoop. So, the ball did not go through the hoop.
Finds the equation of the path traversed by the ball as:
y = − 3/200 x² + 21/20 x + 7.
Write that when x = 70 feet, y = 7 feet. So, the ball went by 7 feet above the floor which means 3 feet below the basketball hoop. So, the ball did not go through the hoop.
Q 19. Answer the questions based on the given information.
The flight path of two aeroplanes in a flight simulator game are shown below. The coordinates of the airports P and Q are given.
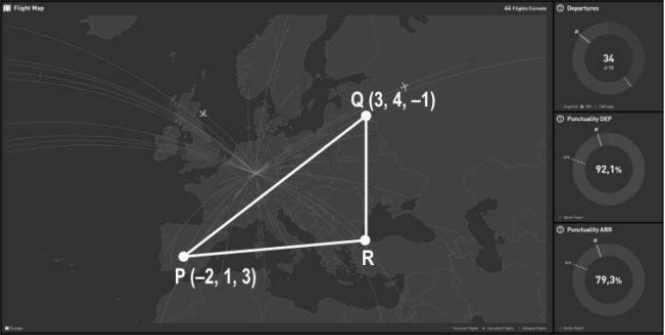 Aeroplane 1 flies directly from P to Q.
Aeroplane 2 has a layover at R and then flies to Q.
Aeroplane 1 flies directly from P to Q.
Aeroplane 2 has a layover at R and then flies to Q.
(Note: Assume that the flight path is straight and fuel is consumed uniformly throughout the flight.)
OR
iii) Consider that Aeroplane 1 started the flight with a full fuel tank. Find the position vector of the point where a third of the fuel runs out if the entire fuel is required for the flight. Show your work. Solution: (i) Writes the vectors for points P and Q as follows: (ii)
Uses vector subtraction to find the vector representing the flight path from R to Q as:
(ii)
Uses vector subtraction to find the vector representing the flight path from R to Q as:
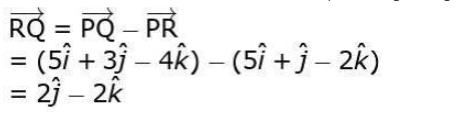 (iii) Finds the cosine of the angle between the vectors representing the flight paths of Aeroplane 1 and Aeroplane 2 as:
(iii) Finds the cosine of the angle between the vectors representing the flight paths of Aeroplane 1 and Aeroplane 2 as:

OR
(iii) Consider a point S which divides PQ internally in the ratio 1:2. Finds the position vector of point S as: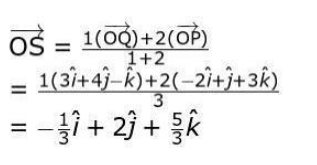 (Award 0.5 marks if only the formula is written correctly.)
(Award 0.5 marks if only the formula is written correctly.)
Q 20. Answer the questions based on the given information. Rubiya, Thaksh, Shanteri, and Lilly entered a spinning zone for a fun game, but there is a twist: they don’t know which spinner will appear on their screens until it is their turn to play. They may encounter one of the following spinners, or perhaps even both:
Different combinations of numbers will lead to exciting prizes. Below are some of the rewards they can win: ♦ Get the number ‘5’, from Spinner A and ‘8’ from Spinner B, and you’ll win a music player! ♦ You win a photo frame if Spinner A lands on a value greater than that of Spinner B!OR

OR
(i) Uses the theorem of total probability and writes: P(getting 2) = [P(Spinner A) × P(Getting 2|Spinner A)] + [P(Spinner B) × P(Getting 2|Spinner B)] Finds the required probability by substituting the required probability as: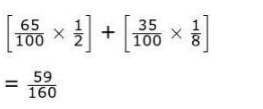
Q 21. Answer the questions based on the given information.
Two metal rods, R1 and R2, of lengths 16 m and 12 m respectively, are insulated at both the ends. Rod R1 is being heated from a specific point while rod R2 is being cooled from a specific point.
The temperature (T) in Celsius within both rods fluctuates based on the distance (x) measured from either end. The temperature at a particular point along the rod is determined by the equations T = (16 – x)x and T = (x – 12)x for rods R1 and R2 respectively, where the distance x is measured in metres from one of the ends.
Show your work
Solution: (i) Identifies that the rod being heated is R1 and finds the rate of change of temperature at any distance from one end of R1 as: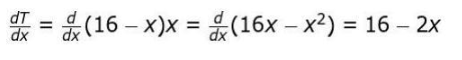 Find the midpoint of the rod as x = 8 m.
Finds the rate of change of temperature at the midpoint of R1 as:
Find the midpoint of the rod as x = 8 m.
Finds the rate of change of temperature at the midpoint of R1 as:
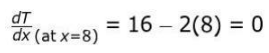 (ii)
Identifies that the rod being cooled is R2 and finds the rate of change of temperature at any distance x m as:
(ii)
Identifies that the rod being cooled is R2 and finds the rate of change of temperature at any distance x m as:
 Finds the minimum temperature attained by the rod R2 as
T(6) = (6 – 12)6 = -36 °C.
Finds the minimum temperature attained by the rod R2 as
T(6) = (6 – 12)6 = -36 °C.
| Cheat Sheets of CBSE Class 12 | |
|---|---|
| Cheat Sheets of CBSE Class 12 Biology | Cheat Sheets of CBSE Class 12 Chemistry |
| Cheat Sheets of CBSE Class 12 English | Cheat Sheets of CBSE Class 12 Mathematics |
