Important Questions for Class 10 Maths Chapter 6 Triangles
Ananya Gupta18 Jan, 2024
Share
Important Questions for Class 10 Maths Chapter 6: Triangles play a crucial role in the exam preparations for students, aligning with the updated CBSE pattern for the 2023-2024 academic session. As students gear up for the board exams, it is strongly recommended that they dedicate focused practice to the important questions related to Triangles.
Scoring full marks in this chapter is attainable through diligent preparation, and these questions serve as a comprehensive resource for achieving that goal. With the potential inclusion of similar questions in the actual exam, students are urged not to overlook any aspect of their preparation. Additional support for comprehensive exam readiness is available through important questions covering all chapters in 10th-grade math at BYJU’S. The Triangles chapter consists of a myriad of topics, including criteria for similarity, congruency, areas of similar triangles, and the Pythagorean theorem. For a thorough understanding and effective exam performance, students can refer to the detailed solutions provided for the important questions in the NCERT solutions for Class 10 Maths. Not only are answers available, but the chapter also offers extra practice questions without solutions, encouraging students to reinforce their grasp on the Triangles topic. By diligently solving these additional problems, students can solidify their command over the subject and enhance their confidence for the upcoming board exams.Important Questions for Class 10 Maths Chapter 6 Triangles Overview
Triangles are essential for students gearing up for their board exams. This chapter covers diverse topics, including the criteria for the similarity of triangles, the Basic Proportionality Theorem (Thales Theorem), proving triangles similar, areas of similar triangles, and the application of the Pythagorean theorem. Carefully created, these important questions offer a strategic approach to exam preparation, ensuring comprehensive coverage of the syllabus and alignment with the CBSE exam pattern.CBSE Important Questions for Class 10 Maths
By solving these questions, students can strengthen their conceptual clarity, master the application of criteria for similarity, and enhance their problem-solving skills in the context of triangles. Accompanied by detailed solutions, these questions facilitate self-assessment, providing a valuable tool for gauging proficiency and rectifying any misconceptions. Utilizing these important questions systematically in their study routine will contribute to a confident and prepared performance in the Class 10 Maths board exams. Physics Wallah teachers are known for providing important questions and valuable resources for Maths subjects. These questions are designed to complement the learning material and aid students in their preparation. Wallah's approach involves imparting not only theoretical knowledge but also practical problem-solving skills. Students are encouraged to solving with these important questions as part of their study routine to reinforce their understanding, practice application of concepts, and prepare effectively for their physics exams.Important Questions & Answers For Class 10 Maths Chapter 6 Triangles
Q.1: In the figure, DE // AC and DF // AE. Prove that BF/FE = BE/EC.
Solution:
Given that, In triangle ABC, DE // AC. By Basic Proportionality Theorem, BD/DA = BE/EC……….(i) Also, given that DF // AE. Again by Basic Proportionality Theorem, BD/DA = BF/FE……….(ii) From (i) and (ii), BE/EC = BF/FE Hence proved.Q.2: In ∆DEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then find the value of DB. (2015)
Solution:
Let BD = x cm then BW = (24 – x) cm, AE = 12 – 4 = 8 cm In ∆DEW, AB || EW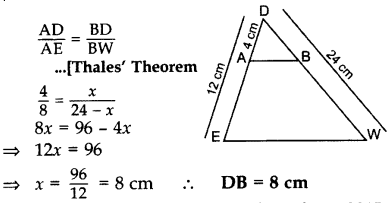
Q.3: In the given figure, PS/SQ = PT/TR and ∠ PST = ∠ PRQ. Prove that PQR is an isosceles triangle.
Solution:
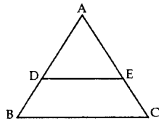
Given, PS/SQ = PT/TR We know that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side. Therefore, ST // QR And ∠ PST = ∠ PQR (Corresponding angles) ……..(i) Also, given, ∠ PST = ∠ PRQ………(ii) From (i) and (ii), ∠ PRQ = ∠ PQR Therefore, PQ = PR (sides opposite the equal angles) Hence, PQR is an isosceles triangle.Q.4: In the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE. (2014)
Solution:
In ∆ADE and ∆ABC, ∠DAE = ∠BAC …Common ∠ADE – ∠ABC … [Corresponding angles ∆ADE – ∆ΑΒC …[AA corollary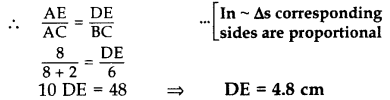
Q.5: In the given figure, altitudes AD and CE of ∆ ABC intersect each other at the point P. Show that:
(i) ∆AEP ~ ∆ CDP (ii) ∆ABD ~ ∆ CBE (iii) ∆AEP ~ ∆ADB (iv) ∆ PDC ~ ∆ BEC
Solution:
Given that AD and CE are the altitudes of triangle ABC and these altitudes intersect each other at P. (i) In ΔAEP and ΔCDP, ∠AEP = ∠CDP (90° each) ∠APE = ∠CPD (Vertically opposite angles) Hence, by AA similarity criterion, ΔAEP ~ ΔCDP (ii) In ΔABD and ΔCBE, ∠ADB = ∠CEB ( 90° each) ∠ABD = ∠CBE (Common Angles) Hence, by AA similarity criterion, ΔABD ~ ΔCBE (iii) In ΔAEP and ΔADB, ∠AEP = ∠ADB (90° each) ∠PAE = ∠DAB (Common Angles) Hence, by AA similarity criterion, ΔAEP ~ ΔADB (iv) In ΔPDC and ΔBEC, ∠PDC = ∠BEC (90° each) ∠PCD = ∠BCE (Common angles) Hence, by AA similarity criterion, ΔPDC ~ ΔBECQ.6: The lengths of the diagonals of a rhombus are 24 cm and 32 cm. Calculate the length of the altitude of the rhombus. (2013)
Solution:
Diagonals of a rhombus are ⊥ bisectors of each other. ∴ AC ⊥ BD, OA = OC = A C 2 ⇒ 24 2 = 12 cm OB = OD = B D 2 ⇒ 32 2 = 16 cm In rt. ∆BOC, Q.7: A boy walks 12 m due east and 5 m due south. How far is he from the starting point ?Options
(a). 31 m (b). 26 m (c). 62 m (d). 13 m
Solution: (b)
Applying Pythagoras’ Theorem
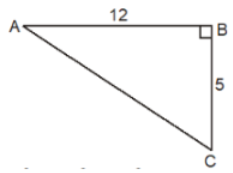
AC 2 =AB 2 +BC 2 ⇒ AC 2 =12 2 +5 2 =144+25=169=13 2 ⇒ AC=13m
Q.8: A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:
Given, Length of the vertical pole = 6 m Shadow of the pole = 4 m Let the height of the tower be h m. Length of the shadow of the tower = 28 m
In ΔABC and ΔDFE,
∠C = ∠E (angle of elevation)
∠B = ∠F = 90°
By AA similarity criterion,
ΔABC ~ ΔDFE
We know that the corresponding sides of two similar triangles are proportional.
AB/DF = BC/EF
6/h = 4/28
h = (6 ×28)/4
h = 6 × 7
h = 42
Hence, the height of the tower = 42 m.
Q.9: The sides AB and AC and the perimeter P, of ∆ABC are respectively three times the corresponding sides DE and DF and the perimeter P, of ∆DEF. Are the two triangles similar? If yes, find a r ( △ A B C ) a r ( △ D E F ) (2012).
Solution:
Given: AB = 3DE and AC = 3DF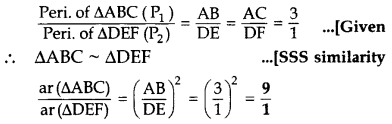
…[∵ The ratio of the areas of two similar ∆s is equal to the ratio of the squares of their corresponding sides.
Q.10: If the areas of two similar triangles are equal, prove that they are congruent.
Solution:
Let ΔABC and ΔPQR be the two similar triangles with equal area.
To prove ΔABC ≅ ΔPQR.
Proof:
ΔABC ~ ΔPQR
∴ Area of (ΔABC)/Area of (ΔPQR) = BC
2
/QR
2
= AB
2
/PQ
2
= AC
2
/PR
2
⇒ BC
2
/QR
2
= AB
2
/PQ
2
= AC
2
/PR
2
= 1 [Since, ar (ΔABC) = ar (ΔPQR)] ⇒ BC
2
/QR
2
= 1
⇒ AB
2
/PQ
2
= 1
⇒ AC
2
/PR
2
= 1
BC = QR
AB = PQ
AC = PR
Therefore, ΔABC ≅ ΔPQR [SSS criterion of congruence]
Q.11: O is any point inside a rectangle ABCD as shown in the figure. Prove that OB 2 + OD 2 = OA 2 + OC 2 .
Solution:
Through O, draw PQ || BC so that P lies on AB and Q lies on DC.
PQ || BC
Therefore, PQ ⊥ AB and PQ ⊥ DC (∠ B = 90° and ∠ C = 90°)
So, ∠ BPQ = 90° and ∠ CQP = 90°
Hence, BPQC and APQD are both rectangles.
By Pythagoras theorem,
In ∆ OPB,
OB
2
= BP
2
+ OP
2
…..(1)
Similarly,
In ∆ OQD,
OD
2
= OQ
2
+ DQ
2
…..(2)
In ∆ OQC,
OC
2
= OQ
2
+ CQ
2
…..(3)
In ∆ OAP,
OA
2
= AP
2
+ OP
2
…..(4)
Adding (1) and (2),
OB
2
+ OD
2
= BP
2
+ OP
2
+ OQ
2
+ DQ
2
= CQ
2
+ OP
2
+ OQ
2
+ AP
2
(since BP = CQ and DQ = AP)
= CQ
2
+ OQ
2
+ OP
2
+ AP
2
= OC
2
+ OA
2
[From (3) and (4)]
Hence proved that OB
2
+ OD
2
= OA
2
+ OC
2
.
Q.12: In the figure, DE || BC. Find the length of side AD, given that AE = 1.8 cm, BD = 7.2 cm and CE = 5.4 cm.
Solution:
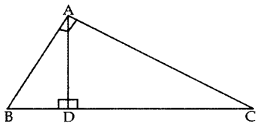
Given, DE || BC AE = 1.8 cm, BD = 7.2 cm and CE = 5.4 cm By basic proportionality theorem, AD/DB = AE/EC AD/7.2 = 1.8/5.4 AD = (1.8 × 7.2)/5.4 = 7.2/4 = 2.4 Therefore, AD = 2.4 cm.Q.13: In the given figure, ∠A = 90°, AD ⊥ BC. If BD = 2 cm and CD = 8 cm, find AD. (2012; 2017D)
Solution:
∆ADB ~ ∆CDA …[If a perpendicular is drawn from the vertex of the right angle of a rt. ∆ to the hypotenuse then As on both sides of the ⊥ are similar to the whole D and to each other ∴ B D A D = A D C D …[∵ Sides are proportional AD 2 = BD , DC AD 2 = (2) (8) = 16 ⇒ AD = 4 cmQ.14: The sides of two similar triangles are in the ratio 7 : 10. Find the ratio of areas of these triangles.
Solution: Given, The ratio of sides of two similar triangles = 7 : 10 We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. The ratio of areas of these triangles = (Ratio of sides of two similar triangles) 2 = (7) 2 : (10) 2 = 49 : 100 Therefore, the ratio of areas of the given similar triangles is 49 : 100.Q.15: In an equilateral ΔABC, D is a point on side BC such that BD = (⅓) BC. Prove that 9(AD) 2 = 7(AB) 2 .
Solution: Given, ABC is an equilateral triangle. And D is a point on side BC such that BD = (1/3)BC. Let a be the side of the equilateral triangle and AE be the altitude of ΔABC.
∴ BE = EC = BC/2 = a/2
And, AE = a√3/2
Given, BD = 1/3BC
∴ BD = a/3
DE = BE – BD = a/2 – a/3 = a/6
In ΔADE, by Pythagoras theorem,
AD
2
= AE
2
+ DE
2
= [(a√3)/2]
2
+ (a/6)
2
= (3a
2
/4) + (a
2
/36)
= (37a
2
+ a
2
)/36
= (28a
2
)/36
= (7/9)a
2
= (7/9) (AB)
2
Therefore, 9(AD)
2
= 7(AB)
2
.
| Download Hand Written Answer Sheets PDF’s | |
| Biology Hand Written Answer Sheets | Maths Hand Written Answer Sheets |
| Chemistry Hand Written Answer Sheets | Physics Hand Written Answer Sheets |
| English Hand Written Answer Sheets | |
Important Questions For Class 10 Maths Chapter 6 Benefits
Conceptual Reinforcement:
- The important questions cover various topics within Chapter 6, providing students with an opportunity to reinforce their understanding of triangle properties and theorems.
Application of Criteria:
- Through solving these questions, students practice applying criteria for similarity, proving triangles similar, and understanding the Basic Proportionality Theorem and the Pythagorean theorem.
Problem-Solving Skills:
- The questions are designed to challenge students and improve their problem-solving skills, encouraging them to think critically and apply concepts in different scenarios.
Self-Assessment:
- Detailed solutions accompanying the questions allow students to self-assess their responses, identify areas of improvement, and rectify any misconceptions.
- Regular self-assessment contributes to a more effective learning process.
Thorough Revision:
- Systematic engagement with these questions ensures a comprehensive revision of key concepts in Chapter 6, enhancing retention and understanding.
| Important Questions for Class 10 Maths Chapter 6 |
| Chapter 1 Real Numbers |
| Chapter 2 Polynomials |
| Chapter 3 Linear Equations In Two Variables |
| Chapter 4 Quadratic Equations |
| Chapter 5 Arithmetic Progression |
| Chapter 6 Triangles |
| Chapter 7 Coordinate Geometry |
| Chapter 8 Introduction to Trigonometry |
| Chapter 9 Applications of Trigonometry |
| Chapter 10 Circles |
| Chapter 11 Constructions |
| Chapter 12 Areas Related to Circles |
| Chapter 13 Surface Areas and Volumes |
| Chapter 14 Statistics |
| Chapter 15 Probability |
Important Questions For Class 10 Maths Chapter 6 FAQs
What is the Side-Side-Side (SSS) Similarity Criterion for triangles?
What does the Basic Proportionality Theorem state?
What are the six main types of triangles in mathematics, and how are they defined?
Explain the concept of congruence in triangles.
State the Pythagorean Theorem.
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
