
NCERT Solutions for Class 10 Maths Chapter 7: In Class 10 Maths Chapter 7, Coordinate Geometry, you'll find solutions to all the exercises in the NCERT textbook. These solutions, created by experts at PW, are great study materials for students getting ready for the CBSE Class 10 board exam. You can easily access and download these solutions.
They provide detailed step-by-step answers to the various types of questions in the NCERT textbook. Practicing these solutions will help you master the topics covered in the coordinate geometry chapter.NCERT Solutions for Class 10 Maths Chapter 7 PDF
You can access the NCERT Solutions for Class 10 Maths Chapter 7 - Coordinate Geometry through the provided PDF link. These solutions offer comprehensive explanations and step-by-step solutions to all the exercises in the chapter. Designed to assist students in their CBSE Class 10 board exam preparation, these solutions are invaluable study materials. They cover various topics such as distance formula, section formula, area of triangles, and more. Click the link below to download the PDF and unlock a valuable resource for mastering Chapter 7 of Class 10 Maths.NCERT Solutions for Class 10 Maths Chapter 7 PDF
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry
NCERT Solutions for Class 10 Maths Chapter 7 on Coordinate Geometry are essential study materials for students preparing for their CBSE board exams. This chapter covers topics such as distance formula, section formula, and the area of triangles using coordinates. The solutions provided offer detailed explanations and step-by-step solutions to help students understand and solve problems related to coordinate geometry. By practicing these solutions, students can strengthen their understanding of the concepts and improve their problem-solving skills.NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Exercise 7.1
1. Find the distance between the following pairs of points:(i) (2, 3), (4,1)
(ii) (–5, 7), (–1, 3)
(iii) (a, b), (–a, –b)
Answer:
(i) Distance between the points is given by
 Therefore the distance between (2,3) and (4,1) is given by
l =
Therefore the distance between (2,3) and (4,1) is given by
l =
 =
=
.png) = √4+4 = √8 = 2√2
= √4+4 = √8 = 2√2
(ii) Applying Distance Formula to find distance between points (–5, 7) and (–1, 3), we get
l = =
=
 = √16+16 = √32 = 4√2
= √16+16 = √32 = 4√2
(iii) Applying Distance Formula to find distance between points (a, b) and (–a, –b), we get
l =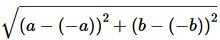 =
=
 =
=
 2. Find the distance between the points (0, 0) and (36, 15). Also, find the distance between towns A and B if town B is located at 36 km east and15 km north of town A.
2. Find the distance between the points (0, 0) and (36, 15). Also, find the distance between towns A and B if town B is located at 36 km east and15 km north of town A.
Answer:
Applying Distance Formula to find distance between points (0, 0) and (36, 15), we get = = √1296 + 225 = √1521 = 39
Yes, we can find the distance between the given towns A and B.
Assume town A at origin point (0, 0).
Therefore, town B will be at point (36, 15) with respect to town A.
And hence, as calculated above, the distance between town A and B will be 39km.
3. Determine if the points (1, 5), (2, 3) and (–2, –11) are collinear.
= √1296 + 225 = √1521 = 39
Yes, we can find the distance between the given towns A and B.
Assume town A at origin point (0, 0).
Therefore, town B will be at point (36, 15) with respect to town A.
And hence, as calculated above, the distance between town A and B will be 39km.
3. Determine if the points (1, 5), (2, 3) and (–2, –11) are collinear.
Answer:
Let A = (1, 5), B = (2, 3) and C = (–2, –11) Using Distance Formula to find distance AB, BC and CA. BC =
BC =
 CA =
CA =
 Since AB+BC ≠ CA
Therefore, the points (1, 5), (2, 3), and (−2, −11) are not collinear.
4. Check whether (5, –2), (6, 4) and (7, –2) are the vertices of an isosceles triangle.
Since AB+BC ≠ CA
Therefore, the points (1, 5), (2, 3), and (−2, −11) are not collinear.
4. Check whether (5, –2), (6, 4) and (7, –2) are the vertices of an isosceles triangle.
Answer:
Let A = (5, –2), B = (6, 4) and C = (7, –2) Using Distance Formula to find distances AB, BC and CA. AB = BC =
BC =
 CA =
CA =
 Since AB = BC.
Therefore, A, B and C are vertices of an isosceles triangle.
5. In a classroom, 4 friends are seated at the points A (3, 4), B (6, 7), C (9, 4) and D (6, 1). Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli. “Don’t you think ABCD is a square?”Chameli disagrees. Using distance formula, find which of them is correct.
Since AB = BC.
Therefore, A, B and C are vertices of an isosceles triangle.
5. In a classroom, 4 friends are seated at the points A (3, 4), B (6, 7), C (9, 4) and D (6, 1). Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli. “Don’t you think ABCD is a square?”Chameli disagrees. Using distance formula, find which of them is correct.

Answer:
We have A = (3, 4), B = (6, 7), C = (9, 4) and D = (6, 1) Using Distance Formula to find distances AB, BC, CD and DA, we get AB = BC =
BC =
 CD =
CD =
 AD =
AD =
 Therefore, All the sides of ABCD are equal here
Now, we will check the length of its diagonals.
Therefore, All the sides of ABCD are equal here
Now, we will check the length of its diagonals.
 AC =
AC =
 BD =
BD =
 So, Diagonals of ABCD are also equal.
we can definitely say that ABCD is a square.
Therefore, Champa is correct.
6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
(i) (–1, –2), (1, 0), (–1, 2), (–3, 0)
(ii) (–3, 5), (3, 1), (0, 3), (–1, –4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
So, Diagonals of ABCD are also equal.
we can definitely say that ABCD is a square.
Therefore, Champa is correct.
6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
(i) (–1, –2), (1, 0), (–1, 2), (–3, 0)
(ii) (–3, 5), (3, 1), (0, 3), (–1, –4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Answer:
(i)Let A = (–1, –2), B = (1, 0), C= (–1, 2) and D = (–3, 0) Using Distance Formula to find distances AB, BC, CD and DA, we get AB = BC =
BC =
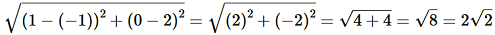 CD =
CD =
 AD =
AD =
.png) Therefore, all four sides of quadrilateral are equal.
Now, we will check the length of diagonals.
AC =
Therefore, all four sides of quadrilateral are equal.
Now, we will check the length of diagonals.
AC =
.png) BD =
BD =
 Therefore, diagonals of quadrilateral ABCD are also equal.
we can say that ABCD is a square.
(ii)Let A = (–3, 5), B= (3, 1), C= (0, 3) and D= (–1, –4)
Using Distance Formula to find distances AB, BC, CD and DA, we get
AB =
Therefore, diagonals of quadrilateral ABCD are also equal.
we can say that ABCD is a square.
(ii)Let A = (–3, 5), B= (3, 1), C= (0, 3) and D= (–1, –4)
Using Distance Formula to find distances AB, BC, CD and DA, we get
AB =
 BC =
BC =
 CD =
CD =
 DA =
DA =
 We cannot find any relation between the lengths of different sides.
Therefore, we cannot give any name to the quadrilateral ABCD.
(iii)Let A = (4, 5), B= (7, 6), C= (4, 3) and D= (1, 2)
Using Distance Formula to find distances AB, BC, CD and DA, we get
AB =
We cannot find any relation between the lengths of different sides.
Therefore, we cannot give any name to the quadrilateral ABCD.
(iii)Let A = (4, 5), B= (7, 6), C= (4, 3) and D= (1, 2)
Using Distance Formula to find distances AB, BC, CD and DA, we get
AB =
 BC =
BC =
 CD =
CD =
 DA =
DA =
 Here opposite sides of quadrilateral ABCD are equal.
We can now find out the lengths of diagonals.
AC =
Here opposite sides of quadrilateral ABCD are equal.
We can now find out the lengths of diagonals.
AC =
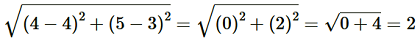 BD =
BD =
 Here diagonals of ABCD are not equal.
we can say that ABCD is not a rectangle therefore it is a parallelogram.
7. Find the point on the x–axis which is equidistant from (2, –5) and (–2, 9).
Here diagonals of ABCD are not equal.
we can say that ABCD is not a rectangle therefore it is a parallelogram.
7. Find the point on the x–axis which is equidistant from (2, –5) and (–2, 9).
Answer:
Let the point be (x, 0) on x–axis which is equidistant from (2, –5) and (–2, 9). Using Distance Formula and according to given conditions we have: ⇒
⇒
 Squaring both sides, we get
⇒
Squaring both sides, we get
⇒
 (x-2)² + 25 = (x+2)² + 81
x² + 4 - 4x + 25 = x² + 4 + 4x + 81
8x = - 25 - 81
8x = -56
x = - 7
Therefore, point on the x–axis which is equidistant from (2, –5) and (–2, 9) is (–7, 0)
8. Find the values of y for which the distance between the points P (2, –3) and Q (10, y) is 10 units.
(x-2)² + 25 = (x+2)² + 81
x² + 4 - 4x + 25 = x² + 4 + 4x + 81
8x = - 25 - 81
8x = -56
x = - 7
Therefore, point on the x–axis which is equidistant from (2, –5) and (–2, 9) is (–7, 0)
8. Find the values of y for which the distance between the points P (2, –3) and Q (10, y) is 10 units.
Answer:
Using Distance formula, we have ⇒
⇒
 ⇒ 64 + (y +3)² = 100
⇒ (y+3)² = 100-64 = 36
⇒ y+3 = ± 6
⇒ y+3=6 or y+3 = - 6
Therefore y = 3 or -9
9. If, Q (0, 1) is equidistant from P (5, –3) and R (x, 6), find the values of x. Also, find the distances QR and PR.
⇒ 64 + (y +3)² = 100
⇒ (y+3)² = 100-64 = 36
⇒ y+3 = ± 6
⇒ y+3=6 or y+3 = - 6
Therefore y = 3 or -9
9. If, Q (0, 1) is equidistant from P (5, –3) and R (x, 6), find the values of x. Also, find the distances QR and PR.
Answer:
It is given that Q is equidistant from P and R. Using Distance Formula, we get PQ = RQ
 ⇒√25+16 = √x² + 25
⇒41 = x² + 25
16 = x²
x = ± 4
Thus, R is (4, 6) or (–4, 6).
When point R is (4,6)
PR =
⇒√25+16 = √x² + 25
⇒41 = x² + 25
16 = x²
x = ± 4
Thus, R is (4, 6) or (–4, 6).
When point R is (4,6)
PR =
 QR =
QR =
 When point R is (- 4,6)
PR =
When point R is (- 4,6)
PR =
 QR =
QR =
 10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (–3, 4).
10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (–3, 4).
Answer:
It is given that (x, y) is equidistant from (3, 6) and (–3, 4). Using Distance formula, we can write ⇒
⇒
 ⇒ (x-3)² + (y-6)² = (x+3)² + (y-4)²
⇒ x² + 9 -6x + y² + 36 - 12y = x² + 9 + 6x + y² + 16 - 8y
⇒36- 16 = 6x + 6x + 12y - 8y
⇒20 = 12x + 4y
⇒3x + y = 5
⇒3x + y - 5 = 0
⇒ (x-3)² + (y-6)² = (x+3)² + (y-4)²
⇒ x² + 9 -6x + y² + 36 - 12y = x² + 9 + 6x + y² + 16 - 8y
⇒36- 16 = 6x + 6x + 12y - 8y
⇒20 = 12x + 4y
⇒3x + y = 5
⇒3x + y - 5 = 0
Related Links -
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Exercise 7.2
1. Find the coordinates of the point which divides the join of (- 1, 7) and (4, - 3) in the ratio 2:3.
Answer: Let P(x, y) be the required point. Using the section formula chapter 7-Coordinate Geometry Exercise 7.2/18.PNG chapter 7-Coordinate Geometry Exercise 7.2/18.PNG Therefore the point is (1,3).2. Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Answer: chapter 7-Coordinate Geometry Exercise 7.2/18.PNG Let P (x1,y1) and Q (x2,y2) are the points of trisection of the line segment joining the given points i.e., AP = PQ = QB Therefore, point P divides AB internally in the ratio 1:2. chapter 7-Coordinate Geometry Exercise 7.2/18.PNG chapter 7-Coordinate Geometry Exercise 7.2/18.PNG Therefore P(x1,y1) = (2, -5/3) Point Q divides AB internally in the ratio 2:1. chapter 7-Coordinate Geometry Exercise 7.2/18.PNG chapter 7-Coordinate Geometry Exercise 7.2/18.PNG Q (x2 ,y2) = (0, -7/3)3. To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in the following figure. Niharika runs 1/4th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flagexactly halfway between the line segment joining the two flags, where should she post her flag?
Answer: chapter 7-Coordinate Geometry Exercise 7.2/18.PNG4. Find the ratio in which the line segment joining the points (-3, 10) and (6, - 8) is divided by (-1, 6).
Answer: Let the ratio in which the line segment joining ( -3, 10) and (6, -8) is divided by point ( -1, 6) be k:1. Therefore, -1 = 6k-3/k+1 -k - 1 = 6k -3 7k = 2 k = 2/7 Therefore, the required ratio is 2:7.5. Find the ratio in which the line segment joining A (1, - 5) and B (- 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.
Answer: Let the ratio in which the line segment joining A (1, - 5) and B ( - 4, 5) is divided by x-axis be k:1. Therefore, the coordinates of the point of division is (-4k+1/k+1, 5k-5/k+1). We know that y-coordinate of any point on x-axis is 0. ∴ 5k-5/k+1 = 0 Therefore, x-axis divides it in the ratio 1:1. To find the coordinates let's substitute the value of k in equation(1) Required point = [(- 4(1) + 1) / (1 + 1), (5(1) - 5) / (1 + 1)] = [(- 4 + 1) / 2, (5 - 5) / 2] = [- 3/2, 0]6. If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Answer: Let A,B,C and D be the points (1,2) (4,y), (x,6) and (3,5) respectively. chapter 7-Coordinate Geometry Exercise 7.2/fig-2.jpg7. Find the coordinates of a point A, where AB is the diameter of circle whose centre is (2, - 3) and B is (1, 4).
Answer:
Let (x,y) be the coordinate of A. Since AB is the diameter of the circle, the centre will be the mid-point of AB. now, as centre is the mid-point of AB. x-coordinate of centre = (2x+1)/2 y-coordinate of centre = (2y+4)/2 But given that centre of circle is (2,−3). Therefore, (2x+1)/2=2⇒x=3 (2y+4)/2=−3⇒y=−10 Thus the coordinate of A is (3,−10).8. If A and B are (–2, –2) and (2, –4), respectively, find the coordinates of P such that AP = 3/7 AB and P lies on the line segment AB.
Answer: As given the coordinates of A(−2,−2) and B(2,−4) and P is a point lies on AB. And AP = 3/7 AB ∴BP = 4/7 Then, ratio of AP and PB = m1:m2 = 3:4 Let the coordinates of P be (x,y). ∴ x = (m1x2 + m2x1) / (m1 + m2) ⇒ x = (3 × 2 + 4 × (−2)) / (3 + 4) = (6 − 8) / 7 = −2 / 7 And y = (m1y2 + m2y1) / (m1 + m2) ⇒ y = ((3 × (−4) + 4 × (−2)) / (3 + 4) = (−12−8) / 7 = −20 / 7 ∴ Coordinates of P = −2 / 7, −20 / 79. Find the coordinates of the points which divide the line segment joining A (- 2, 2) and B (2, 8) into four equal parts.
Answer: chapter 7-Coordinate Geometry Exercise 7.2/fig-4.PNG From the figure, it can be observed that points X,Y,Z are dividing the line segment in a ratio 1:3,1:1,3:1 respectively. Using Sectional Formula, we get, Coordinates of X = ((1 × 2 + 3 × (−2)) / (1 + 3), (1 × 8 + 3 × 2) / (1 + 3)) = (−1, 7/2) Coordinates of Y = (2 − 2) / 2, (2 + 8) / 2 = (0,5) Coordinates of Z = ((3 × 2 + 1 × (−2)) / (1 + 3), (3 × 8 + 1 × 2) / (1 + 3) = (1, 13/2)10. Find the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2,-1) taken in order. [Hint: Area of a rhombus = 1/2(product of its diagonals)]
Answer: Let (3, 0), (4, 5), ( - 1, 4) and ( - 2, - 1) are the vertices A, B, C, D of a rhombus ABCD. Length of the diagonal AC= Length of the diagonal BD= Area of rhombus ABCD = 1/2 X 4√2 X 6√2= 24 square units. Therefore, the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2,-1) taken in order, is 24 square units.NCERT Solutions for Class 10 Maths Chapter 7 FAQs
What is coordinate geometry?
What is the Cartesian coordinate system?
What is the section formula in coordinate geometry?
What is the distance formula in coordinate geometry?













